IGMC: Inductive Matrix Completion based on Graph Neural Networks, ICLR 2020
[Paper Review] IGMC: Inductive Matrix Completion based on Graph Neural Networks, ICLR 2020, Chen et al
Goal
Inductive matrix completion via GNN
Challenge
- MF(Matrix Factorization) is intrinsically transductive
- Low generalization for the unseen users/items
- IMC(Inductive matrix completion) is dependent on content quality
- Leverage side information(content) of users and items
- Scalability challenge
- Require the whole rating matrix $\textbf{R}$
Solution
- Inductive matrix completion via GNN
- Local graph pattern에 집중함으로써 Challenge 2, 3을 완화하려는 전략이다. Observed rating에 대해선 user-item 간에 edge를 추가하여, bipartite graph를 생성한다. 즉, Main task인 Matrix completion을 Link prediction으로 transform하여, unknown rating에 대해 predict하는 방식으로 진행하게 된다.
- Not use any content
- Not need of the whole rating matrix $\textbf{R}$
IDEA 더보기
- LikePath 개념 : 만약 $u_2$가 새로운 item $v_2$를 like했다면, $u_1$도 $v_2$를 like할 가능성이 높다. 왜냐하면, $u_1$과 $u_2$는 같은 취향을 갖고 있기 때문이다.(동일한 item $v_1$을 like했으니). 이러한 path를 like path라고 부른다.
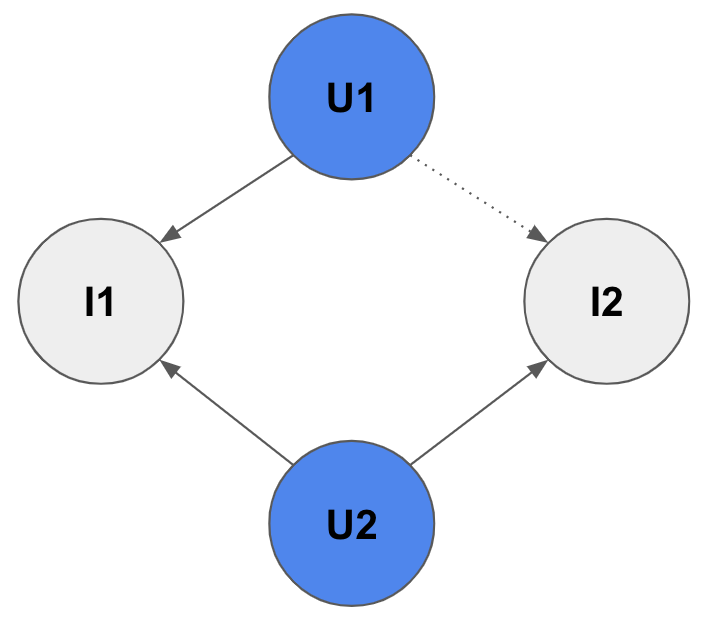
- Traditional Heuristic Link Prediction : 위와 같은 like path 아이디어를 토대로, indicator로서 이런 like path의 갯수를 count하는 등의 휴리스틱한 방식을 사용하여 link prediction을 수행함. link prediction의 목적은, how likely $u_1$ likes $v_2$ 이다.
Method
- Automatic link prediction
- Traditional link prediction은 bipartite graph에 적합하지 않기에, automatic한 link prediction 방법 제안한다. 목적 자체는 traditional link prediction과 동일하다.
- 간략 진행 순서
- Extract $h$-hop enclosing subgraph & Node labeling
- Feed the subgraphs to GNN
- Predict rating of each subgraph : center user -> center item
- Optimization
- Link prediction loss : $L$
- MSE loss between predicted rating and ground-truth rating
- Adjacent rating regularization : $L_{ARR}$
- 기본적으로 rating의 범위가 1~5로 rating 간에 순서가 존재하게 된다. 즉, rating 1,4,5끼리 비교를 하자면, rating 1과 달리 rating 4는 rating 5와 매우 가깝다. 즉, rating 4는 어느정도 interest가 있다고 볼 수 있다는 것이다.
- 그러나 R-GCN에선 애초에 이런 걸 목적으로 했다기 보단, heterogeneity 를 잘 다루겠다는 목적으로 edge type별로 구별한 것이기 때문에 rating 간의 순서를 알지 못한다. 즉, rating 4이던 rating 1이던 마치 하나의 categorical class라고만 볼 뿐, interest의 정도의 차이를 인지하지 못한다.
- 이를 위해, Frobenius norm을 활용해서 adjacent ratings 간에 너무 큰 차이가 나지 않도록 regularize하는 term이다.
- Link prediction loss : $L$
1. Extract $h$-hop enclosing subgraph & Node labeling
- Extraction
- Bipartite subgraph by user-item pair $(u, v)$ and their neighbors within $h$-hop
- Node labeling
- Subgraph 내의 모든 노드들에 대해서 node labeling을 진행한다. 기억해야 할 점은, 1) user와 item 간의 노드 타입 구분 2) Target 노드들과 Else 노드들을 구분 3) 거리 정보 반영 (hop) 의 특징이 있다는 것이다.
Node labeling 더보기
The one-hot encoding of these node labels will be treated as the initial node features $x^0$ of the subgraph when fed to the GNN.
IGMC에서 node labeling을 하는 목적은, global-graph 와 별개로 sub-graph 내부에서 각각의 node에 대한 node-id를 부여하려는 것이다. 즉, global node IDs와는 다르다. Global IDs를 사용하지 않고, Local IDs를 사용하는 이유는, IGMC가 inductive를 지향하고 있기 때문이다. 더불어, 각 노드의 content information을 전혀 사용하지 않고 있는데, 앞서 challenge로 지적했던 IMC는 content quality에 dependent 하다는 문제에 대해서도 이런 방식으로 태클링 하고 있다고 볼 수 있을 것 같다. Side information과 같은 추가적인 content가 없더라도, GNN을 토대로 interaction 정보를 충분히 활용하여 user와 item에 대한 feature를 만들 수 있다는 의도로 해석된다.
구체적인 방법은 다음과 같다. 기본적으로 지금 우리가 관심이 있는 target user와 item은 각각 0과 1을 부여하면서 시작한다. 그리고 subgraph 내의 나머지 노드들에 대해서 user이면 짝수 $2i$ 로, item이면 홀수 $2i+1$ 로 번호를 부여한다. 이때 $i$ 는 hop이다. 즉, target 노드로부터 얼마나 멀리 떨어져 있는지를 고려한다.
2. Feed the subgraphs to GNN
핵심은, 현재 관심이 있는 user와 item 노드를 중심으로 하는 subgraph를 뽑아서, 이 sub-graph에 대한 rating 을 하자는 것이다. 즉, subgraph에 대한 rating이 우리가 관심있는 Target 노드들 간의 rating score로 사용한다. 따라서 node-level이 아니라 graph-level로 접근해야 한다.
또한 인지해야 하는 점이, Full-graph level이 아니라 Sub-graph level이란 점이다. Subgraph 단위로 처리하기 때문에 전체 rating matrix $\textbf{R}$ 를 한꺼번에 입력으로 받을 필요가 없어진다. 이로 인해 Scalability issue를 완화할 수 있게 되겠지만, 그만큼 위에서 서술한 subgraph extraction의 역할이 중요해진다.
Backbone GNN 모델은 R-GCN(Relational Graph Convolutional Operator) 모델을 사용한다. 이름에서도 알 수 있듯이 R-GCN은 GCN을 토대로 heterogeneous graph를 잘 풀어보려는 목적으로 제안된 논문이다. GCN 저자 Thomas Kipf와 Max Welling까지 출동해서 R-GCN을 발표했다. 간단하게 특징들을 정리 해보자면,
1) 가장 중요한 점은 heterogenity를 고려해주기 위해서 edge type 별로 별도의 embedding layer가 존재(relational-specific transformations) 하고, central node와 neighbor node들 간의 embedding layer도 별개이다. R-GCN논문에 따르자면, self-loop을 처리하기 위해 embedding layer를 분리한 것에 대해서 special relation type 으로 본다고 말하고 있다.
2) 그 후엔 GraphSAGE에서 처럼, neighbor nodes에 대한 표현들을 aggregation하여 하나의 이웃벡터 표현을 만든다.
3) 최종적으로, central node 표현과 neighbor node 표현을 더해서 update를 하는 방식으로 진행된다.
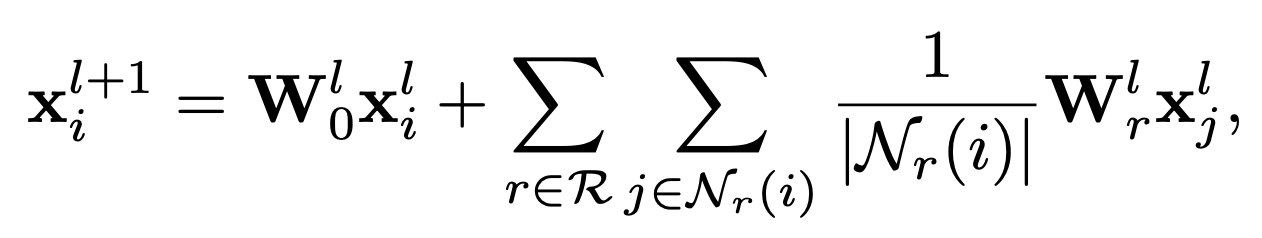
말로 하니까 복잡한 것처럼 보이긴 하는데, 수식으로 보는 것이 역시 간단하다. R-GCN은 3)에서 끝나고 마지막 layer에서의 output을 최종적인 node representation으로 활용하는데 반해, 이 논문에선 각각의 layer에서 나온 feature vector들을 concat하여 중심노드에 대한 최종적인 표현을 얻게 된다. 이때, 우리의 target은 user와 item 노드 두 가지가 있으므로, 얻어야 하는 표현은 $\bf{h}_u, \bf{h}_v$ 두 종류가 된다.
이제 subgraph에 대한 표현을 얻는다.
$\bf{g}=concat(\bf{h}_u, \bf{h}_v)$
3. Predict rating of each subgraph
target user와 item 간의 rating을 얻는다. 이때 중요한 점이, rating의 범위가 1~5 사이의 값이기 때문에 activation function으로 ReLU를 쓴다는 것이다. 아래 식에서 $\sigma$는 ReLU이고, $\hat{r}$은 predicted rating이 된다.
$\hat{r}=\bf{w}^T \sigma(\bf{W}\bf{g})$
ETC.
- Dropdown 기능이 있으니까 너무 행복해서 글이 너무 길어졌다. 쓰다 보니까 자꾸 욕심이 난다. 블로그에선 간단하게 정리만 하고, 자세한 내용은 논문에 남긴 필기를 보면서 리마인드를 하는게 원래의 계획이었는데, 뭐가 좋은지 모르겠다. 이것저것 시도해보고 그때그때 맞는 걸 선택해야 할 듯 하다. R-GCN 얘기하면서 Max Welling도 여기 저자라고 말하는 부분에서 현타가.. ‘간결’에서 한 층 멀어진 글이 되어가고 있음을 느꼈다.
- 심미적인 측면에서, 왜 다른 사람들이 쓴 글은 예뻐보이는데 내가 쓴 글은 못생겨보이는걸까? 다음엔 색깔을 좀 활용해봐야겠다.
- vscode에서 블로그 작업을 하는데, 너무 편하다. 아직까진 대만족이다!
Source
- https://arxiv.org/pdf/1904.12058.pdf
- Inductive Matrix Completion based on Graph Neural Networks, ICLR 2020

Leave a comment